图论及其应用
工科思考:学的东西有什么实际应用,能解决什么问题?与应用关联,对应用敏锐。
学习方法:理解概念,联系应用。一句话表达清楚一个概念。
图模型
利用图建模现实问题,并用图的理论加以解决的能力。
-
婚配问题:偶图匹配
充分必要条件:霍尔定理
-
地图导航
图的基本概念
图是一个有穷系统,在顶点集上定义二元关系(V,R)。描述现实世界的事物,从现实问题抽象到数学问题,解决数学问题后再回到现实问题。
完全图、偶图、补图、正则图
$G=(V,E)是一个(n,q)图$
正则图:每个顶点度数都为n,称为n正则图。
完全图:每个顶点都仅与其余的每一个顶点有一条边连接。即(n-1)正则图,n完全图记为$K_n$
偶图(二部图):所有可被划分为集合内部互不相连的两个顶点集的图,顶点数分别为m和n的偶图记为$K_{m,n}$
补图:顶点相同,边为补集的两个图互为补图。
$0\le deg \space v \le n-1$
子图
生成子图:G的生成子图指包含G全部顶点的子图。 生成:包含全部顶点。
度
$G=(V,E)是一个(p,q)图$,与v关联的边的条数就是v的度。
握手定理:$\sum_{i=0}^{i=n}deg(v_i)=2q$
所有顶点的度数之和是边数的两倍。因为一条边连接两个顶点,对总度数的贡献为2。
推论1:握过奇数次手的人有偶数个。
最大度记号$\triangle$(G),G里度数最大的顶点
最小度记号$\space\delta$(G),G里度数最小的顶点
同构
给一个图的顶点重新命名。一一对应
路、圈、连通
概念
连通是图论最重要的概念。
通道: G=(V,E)顶点和边的交错序列。 $v_0x_1v_1…x_nv_n$称为G的一条通道,称作$v_0v_n$通道,长为边数。特别的,$v_0=v_n$称为闭通道。
迹:G的一条没有重复边的通道。
闭迹:没有重复边的闭通道。
顶点不重复,边也不能重复。顶点不重复是更严格的条件。
路:G的一条没有重复顶点的通道。
闭路(圈):没有重复顶点的闭通道。
几类证明方法
- 演绎
- 反证
- 归纳(与自然数有关)
连通
连通图:$G=(V,E).\space \forall u,v \in V. \space if \space u 与 v间有路,则称G连通.$
怎么判定一个图是连通的?
定理1:$G=(V,E)是(p,q)图。\forall u,v \in V\space if\space uv \notin E,then\space deg(u)+deg(v) \ge p-1,则G连通。$(充分条件)
推论1:任意两个不邻接的顶点,如果两者度数之和大于等于p-1,二者之间必有一条长为2的路。
与实际联系:应用软件的推广,找到两个不邻接的用户,如果二者之间的度数大于等于p-1,可以找到长为2的推广途径,使得推广更有效。
推论2:$G=(V,E)是(p,q)图。\forall v \in V\space ,deg(v)\ge\lceil {p\over 2}\rceil,则G连通。$
圈
判定是否有圈。
图论中最常用证明方法:最长路法。图是有穷系统,必有最长路。
定理2:$G=(V,E)\space \forall v \in V\space ,对其中deg(v)>0的顶点,if\space deg(v)都是偶数,则G中有圈。$
推论:$if\space \delta(G) \ge m \ge 2,则至少有长为m+2的圈。$
实际应用:朋友吃饭安排桌子大小,如果每个朋友都至少有m个朋友,安排m+1大小的桌子,就可以保证每个人的左右两边都是朋友。
定理3:如果两个顶点间至少有两条不同的路,图中必定有圈。
补图
定义:顶点相同,边互补的两个图互为补图.
G的补图表示为$G^c$.
-
若图和自己的补图同构,称为自同构,或自补.
-
补图的意义:在原图不方便讨论的问题,可以在补图中考虑.因为二者.
-
在图论中,这个问题即为:
在六个顶点的无向图或者其补图中,一定存在三角形。
Ramsey理论:求R(m,n),使得具有R(m,n)个顶点的图G中有$k_m$,或$G^c$中有$K_n$.
双图
定义:G=(V,E),存在V的二划分.
本质特征与定义等价,也即充要条件。
定理一:G是双图的充要条件是G中圈的长度为偶数/0.
证明方法:构造法.用题目条件构造出需要的结果,即完成证明.
图兰定理
不等式证明:例如$\le$,先证明$<$,再找特例说明等号成立.
定理三 G=(V,E)是(p,q)图,如果G中没有三角形,则$q\le [{p^2\over 4}]$.完全二部图的时候取等号.
数学归纳法.反证.直接证.
数学归纳法证明,利用条件"没有三角形".

极图理论
一个图G没有子图h时,最多有多少边?
可以解决工兵排雷问题.
欧拉图 欧拉定理
欧拉定理
欧拉(闭)迹:包含图的所有顶点的(闭)迹(迹是不含重复边的通道).
欧拉图:包含欧拉闭迹的图.
定理1(欧拉定理):G是欧拉图的充要条件是G连通且每个顶点的度都是偶数.
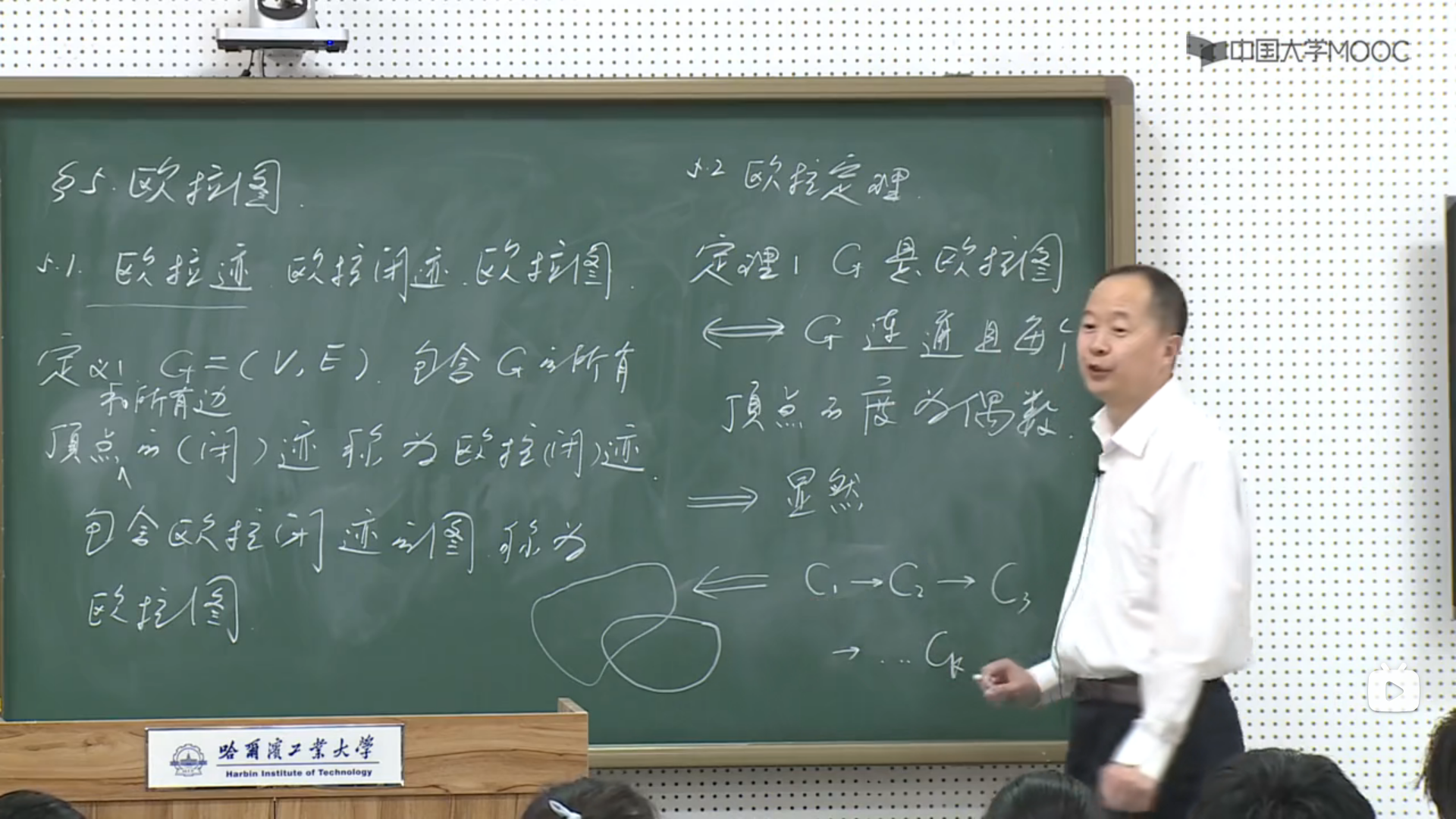
多重图
-
带环图
多重图:两点之间有多条边的图.
带环图:有环的多重图.
定理2(欧拉定理的推广):G中有一条欧拉开迹的充要条件是G中恰有两个奇度顶点.(连上两个奇度顶点就是欧拉闭迹)
定理3 G有2n个奇度顶点,则G至少有n条迹.
哈密顿图
定义:含有生成圈(包含所有顶点的圈)的图.生成圈也称哈密顿圈.
判断方法
判不是
【染色法】对一个图每条边两侧的顶点染不同的颜色,如果这幅图可以完全染色,并且染色后两种颜色的顶点个数不同,则此图一定不是哈密顿图。
*解释:*为了形成生成圈,其两种颜色的顶点必然前后相接并形成圈,因此其个数必然相等。
一个必要条件
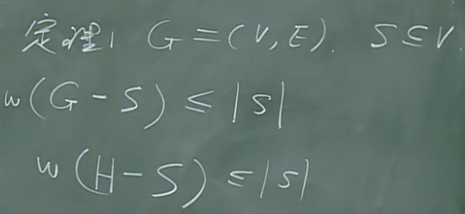
几个充分条件
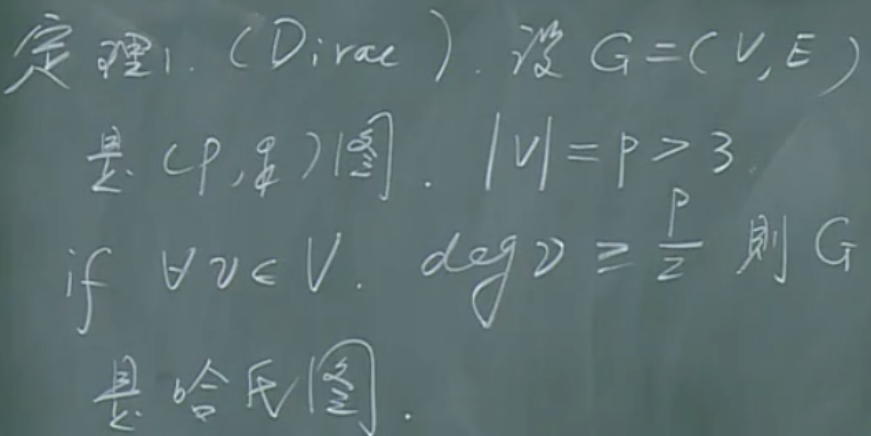
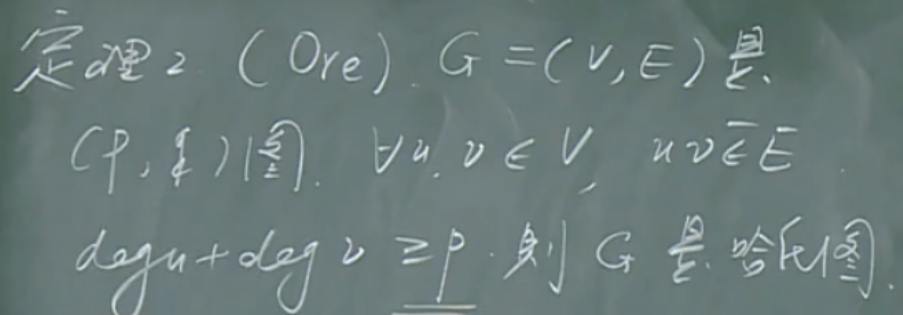

树 割集
现实世界什么信息适合用树表达?
树的定义
定义:一个联通无圈的图称为树,记作$T$.
只有一个顶点的图叫做平凡树.
度为1的顶顶点称作叶子.
非连通无圈图称为森林.
推论1:非平凡树至少有两个叶子.(最长路两个端点的度为1)
推论2:树是双图(G中圈的长度为偶数/0)
树的性质
定理1:设G=(V,E),是(p,q)图,以下命题等价:
- G是树.
- G中任意两个顶点间有唯一的路.
- G是联通的,且p=q+1.(数学归纳法,对p进行归纳)
- G中无圈,且p=q+1.
- G中无圈,且G中任意两个不邻接的顶点加一条边,得到一个有唯一圈的图.
极小连通图
定义:去掉一条边就不连通的图.
定理1:G是树的充要条件是G是极小连通图.
树的中心
距离:两个顶点最短路长度,记为d(u,v。,
e(v)称为v的偏心率,r(G)称为G的半径.
$$
G=(V,E),\forall v\in V,\
e(v)=max_{u\in V}{d(u,v)},\
r(G)=min_{v\in V}{e(v)}
$$
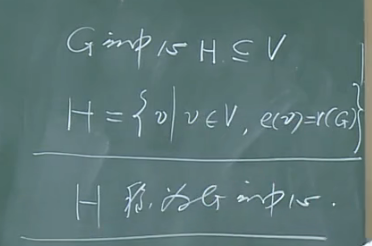
求树的中心:不断去掉叶子,因为去掉叶子前后,树的中心不变,最后剩下一个或两个即为树的中心.
定理:树的中心只能为一个或两个.(最长路法证明)
最小生成树
生成树定义:G=(V,E),G的一个生成子图如果是树,该子图称为生成树.
定理1:G有生成树当且仅当G连通.(破圈法)
最小生成树:带权图,权和最小的生成树.Prim算法和Kruscal算法.管梅谷破圈法.
割点
定义:G=(V,E),v$\in$V,如果 G-v的分支数大于G的分支数,称v为G的一个割点.
定理1:每个非平凡图至少有两个不是割点.(最长路的端点)
定理2:哈密顿图没有割点,有割点的不是哈密顿图.(哈密顿回路是环,有割点说明无环)
割点的性质
(特征性质与定义等价)
以下命题等价:
- v是割点.
- $\exists$u,v$\in$V, u$\ne$w, u,w间的所有路都通过v.
- 存在V\{v}的一个划分{u,w},使得$\forall$u$\in$U,$\forall$w$\in$W, u,w间的路均通过v.

桥
定义:G=(V,E),e$\in$E,如果G-e分支数大于G的分支数,称e为G的桥.
桥的性质
以下命题等价:
- e是割点.
- $\exists$u,v$\in$V, u$\ne$w, u,w间的所有路都包含e.
- 存在E\{e}的一个划分{u,w},使得$\forall$u$\in$U,$\forall$w$\in$W, u,w间的路均包含e.
- e不在任何圈上.
连通度 匹配
连通度的定义
点连通度
连通度指点连通度.
定义:把一个图变成不连通图或平凡图所需要去掉的最少顶点数,记作$k(G)$.
边连通度
定义:把一个图变成不连通图或平凡图所需要去掉的最少边数,记作$\lambda(G)$.
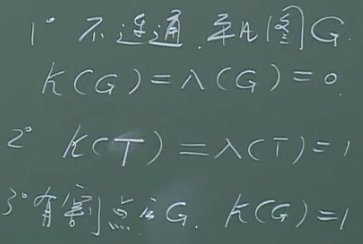
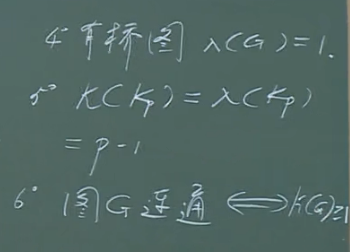
连通度的定理
定理1:G=(V,E),则
$$
k(G)\le \lambda(G)\le \delta(G).
$$
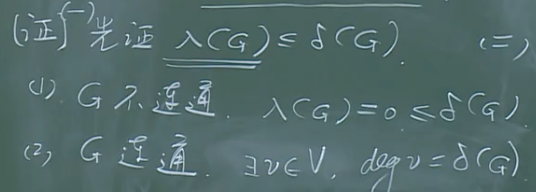
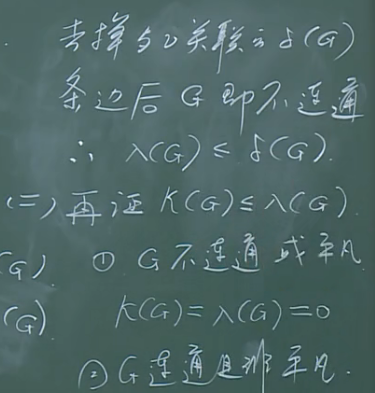
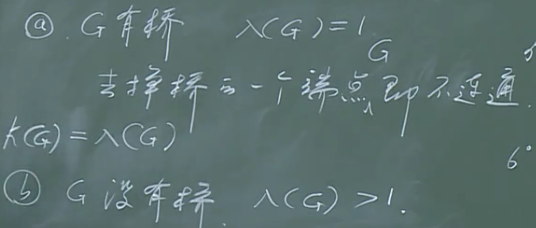
三个刻画图连通度的变量是构建工程网络的约束条件.
定理2:设a,b,c为正整数,$a\le b\le c$,存在G,使得$k(G)=a,\lambda (G)=b,\delta (G)=c$.
用构造法证明.
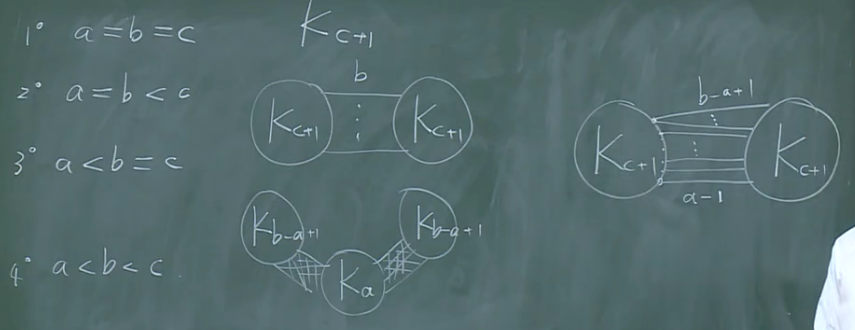
定理3:G=(V,E)是(p,q)图,若$\delta (G) \ge [{p\over 2}]$,则$\lambda (G) = \delta (G)$.
n连通
描述一类图的连通程度.
定义:设G=(V,E),n$\ge$0,如果$k(G)\ge n$,则G为n(点)连通;如果$\lambda(G) \ge n$,则G为n边连通.
定理1:G=(V,E),|V|$\ge$3,G是2连通的 充要条件是 G的任两个不同顶点u和v在G的同一个圈上.(图G没有割点)
定理2:G是n边连通的的 充要条件 是不存在V的真子集A使得连接A中一个结点和V\A中一个结点的边的总数少于n.
明格尔定理
连通问题.
核心思想:u和v之间不同路的条数能反映图G的连通程度.
分离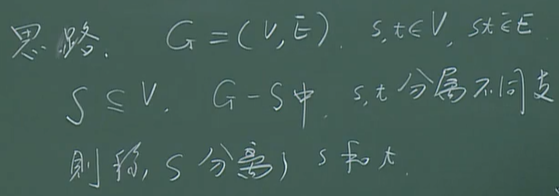
独立轨:两顶点间不相交的路.
明格尔定理:分离s,t所需去掉的最小顶点数等于s,t间不相交的路(独立轨)的最大条数.
分离s,t所需去掉的最小边数等于s,t间边不相交的路(独立轨)的最大条数.
柯尼希定理
匹配问题.
每个正则二部图有一个一度因子(有完美匹配).
每个k正则二部图都能分解出k个一因子.
网络流问题
D=(V,A,W)带权有向图,流就是权(容量).
迭代求解.
流量 容量
网络流:流的集合
可行流:满足平衡条件–流入流出总量相等;现实条件–流量小于容量.
零流
伪流:满足现实条件不满足平衡条件.
最大流:可行流的最大流量总和.
饱和弧:流量和容量相等.
链:不考虑方向的路.
增广路:满足以下条件的链.
- 前向弧不饱和
- 后向弧不是0.
残留流量:容量减去流量.
残留网络:标上残留流量的网络.
割:这里指的的割边.使得图像不连通所需去掉的最小边数.
最小割:最小容量的割.
增广路定理:容量网络中的一条可行流是最大流当且仅当不存在增广路.
最大流最小割定理:容量网络中最大流等于最小割.
匹配问题
独立集 团

最大独立集:所有 I 中顶点数最大的集合.
NP问题总结(概念+例子+证明)_a12638915的博客-CSDN博客
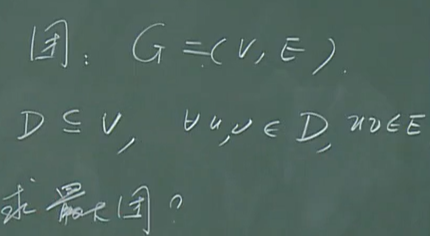
偶图的匹配
边独立集
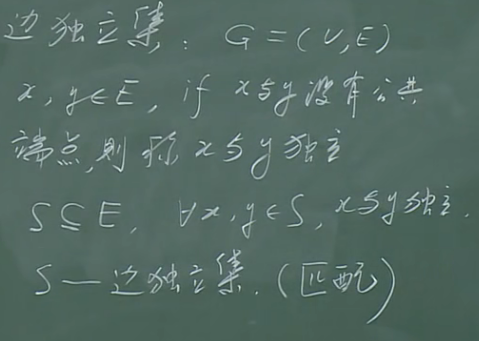
偶图的匹配
S记为偶图的匹配集.
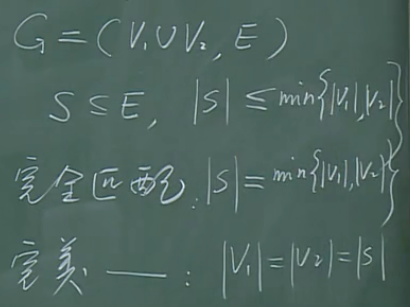
偶图匹配的条件
定理1(Hall的结婚定理):m个姑娘,n个小伙子,每个人都有自己中意的对象列表.m个姑娘在一夫一妻制下全能嫁出去的充要条件.
覆盖 支配集

偶图的性质
- 最大匹配数等于最小覆盖数
- 最大的边覆盖数等于最大独立集数 等于 顶点总数 减去 最大匹配数
平面图
定义
实际应用有印刷电路板,管道系统等等
可平面图和平面图定义.
平面图就是画好的可平面图.
学图论就要学图的特征.平面图的特征是面.

面:内部面和外部面.
面与围成它的边有关.圈里面的是内部面,内部面无边;圈外的是外部面.面与边有紧密的联系.
一条边参与两个面.
欧拉公式
p-q+d=2.
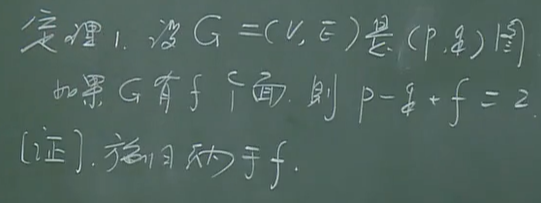

图的着色(顶点)
色数
一条边的两个端点不能着相同的颜色.
n-可着色:有n种颜色可以着色的.最少的n称为色数.
例子:考试安排
色数记为$k$.
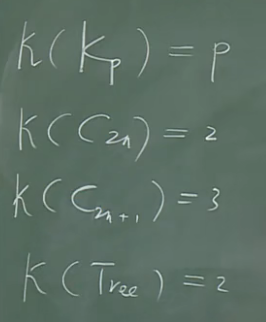
色数上下界
G是(p,q)图,$\delta$(G)是最小度数,$\triangle$(G)是最大度数.
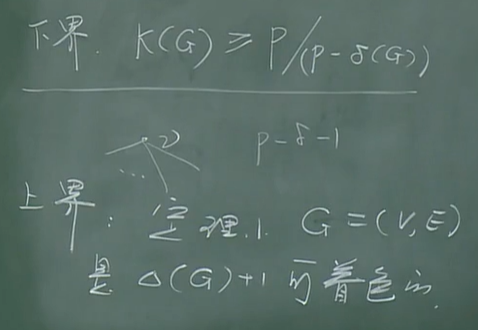
G是平面图,都是$\triangle$(G)可着色的.
每一个(可)平面图是6可着色的.
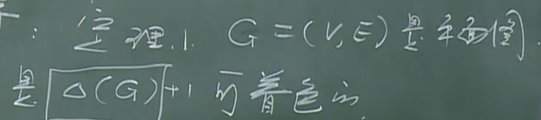
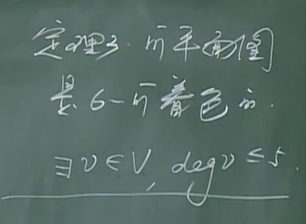
四色定理 五色定理
五色定理的证明

